32. Rekursion¶
A child couldn't sleep, so her mother told her a story about a little frog,
who couldn't sleep, so the frog's mother told her a story about a little bear,
who couldn't sleep, so the bear's mother told her a story about a little weasel...
who fell asleep.
...and the little bear fell asleep;
...and the little frog fell asleep;
...and the child fell asleep.
(Quelle: http://everything2.com/title/recursion)
Als rekursiv definiert bezeichnet man, wenn sich ein Objekt oder ein Prozess mit sich selbst definiert ist. Mathematische Strukturen wie die Fakultät und die Fibonacci-Zahlen kann man rekursiv definieren. Dokumente, die andere Dokumente enthalten können, die selbst andere Dokumente enthalten können, sind rekursiv. Fraktale Bilder und sogar bestimmte biologische Prozesse funktionieren rekursiv.
32.1. Wo wird Rekursion verwendet?¶
Dokumente wie Webseiten sind natürlich rekursiv. Zum Beispiel zeigt Abbildung 20.1 ein einfaches Webdokument.
Abbildung 20.1: Webseite¶
Dieses Webdokument kann in einer „Box“ enthalten sein, die hilft das Layout der Seite aufzubauen (siehe Abbildung 20.2).
Abbildung 20.2: Webseite mit Tabellen¶
Dies funktioniert rekursiv. Jede Box kann eine Webseite enthalten, die eine Box enthalten kann, das eine andere Webseite enthalten kann, wie in Abbildung 20.3 dargestellt.
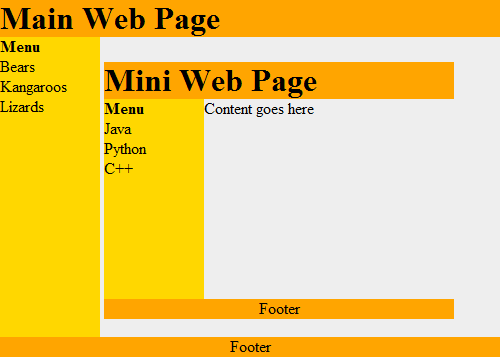
Abbildung 20.3: Webseite mit Rekursion¶
Die komplizierteren Such- und Sortieralgorithmen beschreibt man oft mit rekursiven Funktionen. Wir werden einiges davon hier zeigen und wenn du einen Kurs zu Datenstrukturen belegt, wirst du viel mehr davon sehen.
Auch wenn jemand kein Programmierer wird, ist es wichtig, das Konzept rekursiver Systeme zu verstehen. Wenn eine geschäftliche Anforderung an rekursiven Tabellenstrukturen, Dokumenten oder etwas anderem besteht, ist es wichtig zu wissen, wie man dies für einen Programmierer spezifizieren kann.
Beispielsweise kann jemand angeben, dass ein Webprogramm für Rezepte die Fähigkeit benötigt, Zutaten und Anweisungen zu unterstützen. Jemand, der mit Rekursion vertraut ist, könnte angeben, dass jede Zutat selbst wieder ein Rezept mit anderen Zutaten sein könnte (das könnten dann wieder Rezepte sein). Die zweite Beschreibung ist erheblich leistungsfähiger.
32.2. Wie programmiert man mit Rekursion?¶
In früheren Kapiteln haben wir Funktionen verwendet, die andere Funktionen aufrufen. Zum Beispiel:
1 2 3 4 5 6 7 8 | def f():
g()
print("f")
def g():
print("g")
f()
|
Es ist auch möglich, dass eine Funktion sich selbst aufruft. Eine Funktion, die sich selbst aufruft, verwendet Rekursion. Zum Beispiel:
1 2 3 4 5 | def f():
print("Hello")
f()
f()
|
Das obige Beispiel gibt „Hello“ aus und ruft dann die Funktion f() erneut auf. Dadurch wird ein weiteres „Hello“ ausgegeben und die Funktion f() erneut aufgerufen. Dies wird so lange fortgesetzt, bis dem Rechner der Speicherplatz für den Stack ausgeht. In diesem Fall gibt Python einen langen Fehler aus, der so endet:
RuntimeError: maximum recursion depth exceeded
Der Rechner sagt dir, dem Programmierer, dass du wie Alice zu weit in den Kaninchenbau gekrochen bist.
32.3. Rekursionstiefe steuern¶
Man muss verhindern, dass sich die Funktion endlos immer wieder aufruft, damit man mit Rekursion erfolgreich ein Problem lösen kann. Im folgenden Beispiel wird mitgezählt, wie oft die Funktion aufgerufen wurde, und verwendet eine if-Anweisung, um das Programm zu beenden, sobald die Funktion sich selbst zehnmal aufgerufen hat.
1 2 3 4 5 6 7 8 9 10 11 | def f(level):
# Print the level we are at
print("Recursion call, level",level)
# If we haven't reached level ten...
if level < 10:
# Call this function again
# and add one to the level
f(level+1)
# Start the recursive calls at level 1
f(1)
|
1 2 3 4 5 6 7 8 9 10 | Recursion call, level 1
Recursion call, level 2
Recursion call, level 3
Recursion call, level 4
Recursion call, level 5
Recursion call, level 6
Recursion call, level 7
Recursion call, level 8
Recursion call, level 9
Recursion call, level 10
|
32.4. Rekursion in der Mathematik¶
32.4.1. Fakultät rekursiv berechnen¶
Jeder Code, der rekursiv ausgeführt werden kann, kann auch ohne Verwendung von Rekursion definiert werden. Einige Programmierer finden, dass der rekursive Code leichter zu verstehen ist.
Die Berechnung der Fakultät einer Zahl ist ein klassisches Beispiel für die Verwendung der Rekursion. Die Fakultät ist nützlich für die Wahrscheinlichkeitsrechnung und Statistik. Zum Beispiel:
Rekursiv kann dies so beschrieben werden:
Nachfolgend finden Sie zwei Beispielfunktionen, die das berechnen. Die erste ist nicht rekursiv, der zweite ist rekursiv definiert.
1 2 3 4 5 6 7 | # This program calculates a factorial
# WITHOUT using recursion
def factorial_nonrecursive(n):
answer = 1
for i in range(2, n + 1):
answer = answer * i
return answer
|
1 2 3 4 5 6 7 | # This program calculates a factorial
# WITH recursion
def factorial_recursive(n):
if n == 1:
return 1
elif n > 1:
return n * factorial_recursive(n - 1)
|
Die Funktionen tun nichts von sich aus. Nachfolgend findet sich ein Beispiel, in dem wir alles zusammenfassen. Dieses Beispiel fügt auch einige print-Anweisungen in die Funktion ein, damit wir sehen können, was passiert.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | # This program calculates a factorial
# WITHOUT using recursion
def factorial_nonrecursive(n):
answer = 1
for i in range(2, n + 1):
print(i, "*", answer, "=", i * answer)
answer = answer * i
return answer
print("I can calculate a factorial!")
user_input = input("Enter a number:")
n = int(user_input)
answer = factorial_nonrecursive(n)
print(answer)
# This program calculates a factorial
# WITH recursion
def factorial_recursive(n):
if n == 1:
return 1
else:
x = factorial_recursive(n - 1)
print( n, "*", x, "=", n * x )
return n * x
print("I can calculate a factorial!")
user_input = input("Enter a number:")
n = int(user_input)
answer = factorial_recursive(n)
print(answer)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | I can calculate a factorial!
Enter a number:7
2 * 1 = 2
3 * 2 = 6
4 * 6 = 24
5 * 24 = 120
6 * 120 = 720
7 * 720 = 5040
5040
I can calculate a factorial!
Enter a number:7
2 * 1 = 2
3 * 2 = 6
4 * 6 = 24
5 * 24 = 120
6 * 120 = 720
7 * 720 = 5040
5040
|
32.4.2. Rekursive Ausdrücke¶
Angenommen, du hast einen mathematischen Ausdruck wie diesen:
\(f_{n} = \begin{cases} 6 & \text{if } n = 1, \\ \frac{1}{2}f_{n-1}+4 & \text{if } n > 1. \end{cases}\)
Sieht kompliziert aus, bedeutet aber nur, dass wir für \(n = 1\) \(f_{1}\) verwenden. Diese Funktion gibt eine 6 zurück.
Für \(f_{2}\) geben wir zurück \(\frac{1}{2}f_{1}+4\).
Der Code würde beginnen mit:
1 | def f(n):
|
Dann müssen wir diesen ersten Fall hinzufügen:
1 2 3 | def f(n):
if n == 1:
return 6
|
Siehst du, wie genau die mathematische Notation befolgt wird. Nun zum Rest:
1 2 3 4 5 | def f(n):
if n == 1:
return 6
elif n > 1:
return (1 / 2) * f(n - 1) + 4
|
Das Konvertieren dieser Arten von mathematischen Ausdrücken in Code ist unkompliziert. Aber wir sollten es besser an einem vollständigen Beispiel ausprobieren:
1 2 3 4 5 6 7 8 9 10 11 12 13 | def f(n):
if n == 1:
return 6
elif n > 1:
return (1 / 2) * f(n - 1) + 4
def main():
result = f(10)
print(result)
main()
|
32.5. Rekursive Grafiken¶
32.5.1. Rekursive Rechtecke¶
Rekursion ist ideal, um mit strukturierten Dokumenten zu arbeiten, die selbst rekursiv sind. Beispielsweise kann ein Webdokument eine Tabelle enthalten, die zur Unterstützung des Layouts in Zeilen und Spalten unterteilt ist. Eine Zeile könnte die Kopfzeile, eine andere Zeile der Hauptteil und schließlich die Fußzeile sein. In einer Tabellenzelle befindet sich möglicherweise eine andere Tabelle. Und darin kann noch eine Tabelle existieren.
Ein weiteres Beispiel ist E-Mail. Es ist möglich, die E-Mail einer anderen Person an eine eigene E-Mail anzuhängen. Aber an diese E-Mail könnte eine andere E-Mail angehängt aein, und so weiter.
Can we visually see recursion in action in one of our Pygame programs? Yes! Figure 19.4 shows an example program that draws a rectangle, and recursively keeps drawing rectangles inside of it. Each rectangle is 20% smaller than the parent rectangle. Look at the code. Pay close attention to the recursive call in the recursive_draw function.
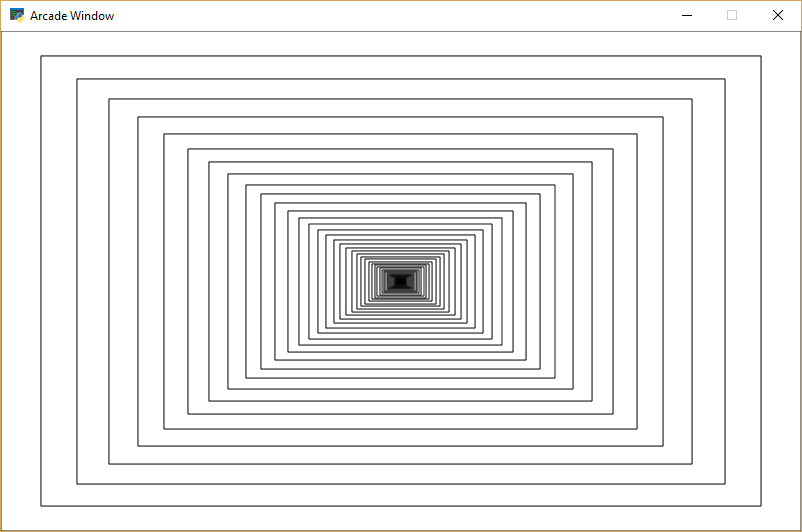
Abbildung 20.4: Rekursive Rechtecke¶
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 | """
Recursive Rectangles
"""
import arcade
SCREEN_WIDTH = 800
SCREEN_HEIGHT = 500
def draw_rectangle(x, y, width, height):
""" Recursively draw a rectangle, each one a percentage smaller """
# Draw it
arcade.draw_rectangle_outline(x, y, width, height, arcade.color.BLACK)
# As long as we have a width bigger than 1, recursively call this function with a smaller rectangle
if width > 1:
# Draw the rectangle 90% of our current size
draw_rectangle(x, y, width * .9, height * .9)
class MyWindow(arcade.Window):
""" Main application class. """
def __init__(self, width, height):
super().__init__(width, height)
arcade.set_background_color(arcade.color.WHITE)
def on_draw(self):
""" Render the screen. """
arcade.start_render()
# Find the center of our screen
center_x = SCREEN_WIDTH / 2
center_y = SCREEN_HEIGHT / 2
# Start our recursive calls
draw_rectangle(center_x, center_y, SCREEN_WIDTH, SCREEN_HEIGHT)
def main():
MyWindow(SCREEN_WIDTH, SCREEN_HEIGHT)
arcade.run()
if __name__ == "__main__":
main()
|
32.5.2. Fraktale¶
Fraktale werden rekursiv definiert. Hier ist ein sehr einfaches Fraktal, das beispielhaft zeigt, wie es sich mit der „Rekursionstiefe“ ändert.

Abbildung 20.5: Rekursives Fraktal Tiefe 0¶
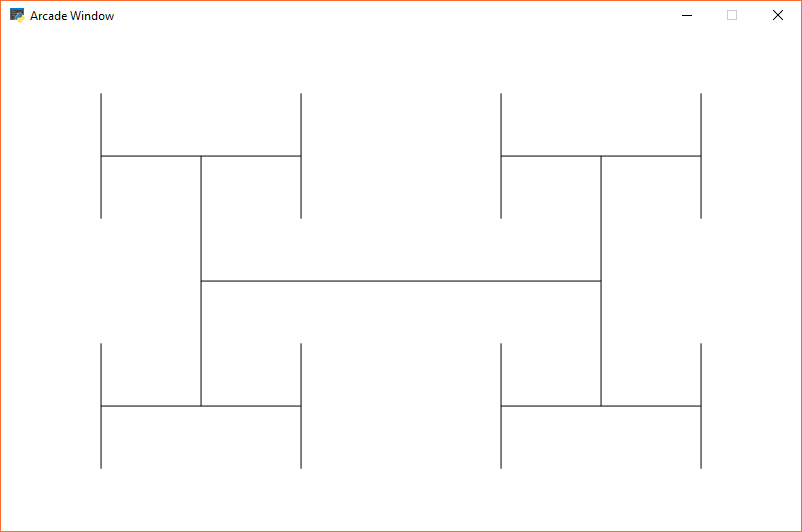
Abbildung 20.6: Rekursives Fraktal Tiefe 1¶
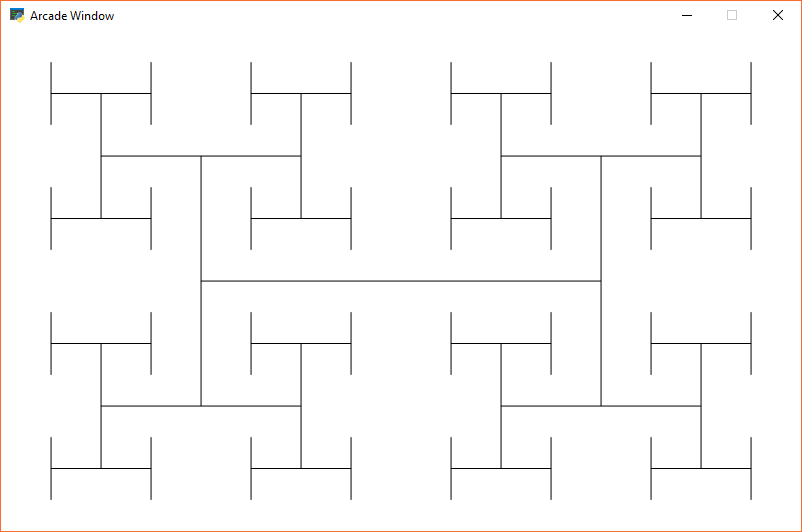
Abbildung 20.7: Rekursives Fraktal Tiefe 2¶

Abbildung 20.8: Rekursives Fraktal Tiefe 5¶
Hier ist der Quellcode für das „H“-Fraktal:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 | """
Recursive H's
"""
import arcade
SCREEN_WIDTH = 800
SCREEN_HEIGHT = 500
RECURSION_DEPTH = 0
def draw_h(x, y, width, height, count):
""" Recursively draw an H, each one a half as big """
# Draw the H
# Draw cross-bar
arcade.draw_line(x + width * .25, height / 2 + y,
x + width * .75, height / 2 + y, arcade.color.BLACK)
# Draw left side
arcade.draw_line(x + width * .25, height * .5 / 2 + y,
x + width * .25, height * 1.5 / 2 + y, arcade.color.BLACK)
# Draw right side
arcade.draw_line(x + width * .75, height * .5 / 2 + y,
x + width * .75, height * 1.5 / 2 + y, arcade.color.BLACK)
# As long as we have a width bigger than 1, recursively call this function with a smaller rectangle
if count > 0:
count -= 1
# Draw the rectangle 90% of our current size
# Draw lower left
draw_h(x, y, width / 2, height / 2, count)
# Draw lower right
draw_h(x + width / 2, y, width / 2, height / 2, count)
# Draw upper left
draw_h(x, y + height / 2, width / 2, height / 2, count)
# Draw upper right
draw_h(x + width / 2, y + height / 2, width / 2, height / 2, count)
class MyWindow(arcade.Window):
""" Main application class. """
def __init__(self, width, height):
super().__init__(width, height)
arcade.set_background_color(arcade.color.WHITE)
def on_draw(self):
""" Render the screen. """
arcade.start_render()
# Start our recursive calls
draw_h(0, 0, SCREEN_WIDTH, SCREEN_HEIGHT, RECURSION_DEPTH)
def main():
MyWindow(SCREEN_WIDTH, SCREEN_HEIGHT)
arcade.run()
if __name__ == "__main__":
main()
|
Du kannst Fraktale online erkunden:
Wenn du deine eigenen Fraktale programmieren möchtest, kannst du mit Hilfe des Kapitel 8 von The Nature of Code von Daniel Shiffman Ideen zu einfachen Fraktalen bekommen.
32.6. Rekursive Labyrinthe¶
Es gibt Algorithmen zur Generierung von Labyrinthen. Wikipedia hat einen schönen Maze generation algorithm-Artikel, der einige Details enthält, aber leider zur Zeit nicht in Deutsch übersetzt ist. Eine Möglichkeit ist die Methode der rekursiven Aufteilung.
Der Algorithmus wird unten beschrieben. Die Bilder stammen aus der Wikipedia.
Beginne mit dem Raum des Labyrinths nur mit den Außenwänden. Nenne das eine Kammer.¶
Teile die Kammer durch eine zufällige horizontale Wand und eine zufällige vertikale Wand.¶
Wähle drei der vier Wände aus und setze eine zufällige positionierte Öffnung hinein.¶
Unterteile jeden der vier Abschnitte. Nenne sie jeweils eine Kammer. Rufe diese Funktion rekursiv auf. In diesem Bild wurde die obere linke Kammer unterteilt.¶
Fertiges Labyrinth.¶
Diese Methode führt zu Labyrinthen mit langen geraden Wänden, die ihren Raum kreuzen, wodurch leichter erkennbar wird, welche Bereiche vermieden werden müssen.

Rekursive Labyrinth-Generierung. Quelle: Wikipedia Maze generation algorithm.¶
Hier ist ein Beispiel in Python, der mit dieser Methode ein Labyrinth erstellt:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 | import random
# These constants are used to determine what should be stored in the grid if we have an empty
# space or a filled space.
EMPTY = " "
WALL = "XXX"
# Maze must have an ODD number of rows and columns.
# Walls go on EVEN rows/columns.
# Openings go on ODD rows/columns
MAZE_HEIGHT = 51
MAZE_WIDTH = 51
def create_grid(width, height):
""" Create an empty grid. """
grid = []
for row in range(height):
grid.append([])
for column in range(width):
grid[row].append(EMPTY)
return grid
def print_maze(maze):
""" Print the maze. """
# Loop each row, but do it in reverse so 0 is at the bottom like we expect
for row in range(len(maze) - 1, -1, -1):
# Print the row/y number
print(f"{row:3} - ", end="")
# Loop the row and print the content
for column in range(len(maze[row])):
print(f"{maze[row][column]}", end="")
# Go down a line
print()
# Print the column/x at the bottom
print(" ", end="")
for column in range(len(maze[0])):
print(f"{column:3}", end="")
print()
def create_outside_walls(maze):
""" Create outside border walls."""
# Create left and right walls
for row in range(len(maze)):
maze[row][0] = WALL
maze[row][len(maze[row])-1] = WALL
# Create top and bottom walls
for column in range(1, len(maze[0]) - 1):
maze[0][column] = WALL
maze[len(maze[0]) - 1][column] = WALL
def create_maze(maze, top, bottom, left, right):
"""
Recursive function to divide up the maze in four sections
and create three gaps.
Walls can only go on even numbered rows/columns.
Gaps can only go on odd numbered rows/columns.
Maze must have an ODD number of rows and columns.
"""
# Figure out where to divide horizontally
start_range = bottom + 2
end_range = top - 1
y = random.randrange(start_range, end_range, 2)
# Do the division
for column in range(left + 1, right):
maze[y][column] = WALL
# Figure out where to divide vertically
start_range = left + 2
end_range = right - 1
x = random.randrange(start_range, end_range, 2)
# Do the division
for row in range(bottom + 1, top):
maze[row][x] = WALL
# Now we'll make a gap on 3 of the 4 walls.
# Figure out which wall does NOT get a gap.
wall = random.randrange(4)
if wall != 0:
gap = random.randrange(left + 1, x, 2)
maze[y][gap] = EMPTY
if wall != 1:
gap = random.randrange(x + 1, right, 2)
maze[y][gap] = EMPTY
if wall != 2:
gap = random.randrange(bottom + 1, y, 2)
maze[gap][x] = EMPTY
if wall != 3:
gap = random.randrange(y + 1, top, 2)
maze[gap][x] = EMPTY
# Print what's going on
print(f"Top/Bottom: {top}, {bottom} Left/Right: {left}, {right} Divide: {x}, {y}")
print_maze(maze)
print()
# If there's enough space, to a recursive call.
if top > y + 3 and x > left + 3:
create_maze(maze, top, y, left, x)
if top > y + 3 and x + 3 < right:
create_maze(maze, top, y, x, right)
if bottom + 3 < y and x + 3 < right:
create_maze(maze, y, bottom, x, right)
if bottom + 3 < y and x > left + 3:
create_maze(maze, y, bottom, left, x)
def main():
# Create the blank grid
maze = create_grid(MAZE_WIDTH, MAZE_HEIGHT)
# Fill in the outside walls
create_outside_walls(maze)
# Start the recursive process
create_maze(maze, MAZE_HEIGHT - 1, 0, 0, MAZE_WIDTH - 1)
if __name__ == "__main__":
main()
|
32.7. Rekursive binäre Suche¶
Die Rekursion kann auch zur Durchführung einer binären Suche verwendet werden. Hier ist eine nicht rekursive binäre Suche aus Kapitel 15:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | def binary_search_nonrecursive(search_list, key):
lower_bound = 0
upper_bound = len(search_list) - 1
found = False
while lower_bound < upper_bound and found == False:
middle_pos = (lower_bound + upper_bound) // 2
if search_list[middle_pos] < key:
lower_bound = middle_pos + 1
elif search_list[middle_pos] > key:
upper_bound = middle_pos
else:
found = True
if found:
print( "The name is at position",middle_pos)
else:
print( "The name was not in the list." )
binary_search_nonrecursive(name_list,"Morgiana the Shrew")
|
Dieselbe binäre Suche, rekursiv geschrieben:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | def binary_search_recursive(search_list, key, lower_bound, upper_bound):
middle_pos = (lower_bound + upper_bound) // 2
if search_list[middle_pos] < key:
# Recursively search top half
binary_search_recursive(search_list, key,
middle_pos + 1, upper_bound)
elif search_list[middle_pos] > key:
# Recursively search bottom half
binary_search_recursive(search_list, key,
lower_bound, middle_pos )
else:
print("Found at position", middle_pos)
lower_bound = 0
upper_bound = len(name_list) - 1
binary_search_recursive(name_list, "Morgiana the Shrew",
lower_bound, upper_bound)
|